This post is inspired by PyQuantNews article on this page.
I have tested the same script with a few twist to better understand the hedging concept.
A Quick Guide to Simple Portfolio Hedging in Volatile Markets**
Beta ($ \beta $) measures the portfolio’s sensitivity to movements in its benchmark. For instance, a portfolio with a $ \boldsymbol\beta $ of 5 would decrease by 5% for every 1% drop in the benchmark, reflecting high sensitivity to market movements.
Prepare the Portfolio and Benchmark performance
We’ll use a few python libraries to gather historical stock data for the “Magnificent 7” mega-cap tech stocks from Yahoo Finance, and then we’ll start by calculating the daily returns, setting up a foundation for analyzing the portfolio’s relationship with its benchmark.
To prepare for this, we separate the benchmark ETF (QQQ) from the portfolio. We calculate daily returns as the percentage change in the adjusted closing prices for both the benchmark and our portfolio stocks.
Analyzing Sensitivity with Linear Regression:
Next, we apply linear regression to understand how our portfolio returns move relative to the benchmark’s returns. This step helps us evaluate how our portfolio’s performance aligns with market trends, providing insights into its market-driven risks. The model summary offers additional statistics to assess the accuracy and reliability of this relationship.
Constructing a Hedged Portfolio:
With the beta value from our regression, we create a hedged portfolio by adjusting the portfolio returns to reduce sensitivity to the benchmark. We then plot the returns of this hedged portfolio alongside the benchmark, allowing us to visually compare performance and see the impact of beta-adjusted hedging.
Calculate and plot the Cumulative Returns
Now that we’ve observed a reduction in volatility when hedging the benchmark in the previous example, let’s move on to compare the cumulative returns of these two different portfolios. This will help us understand the overall impact of hedging on the portfolio’s cumulative performance over time.
Interpreting Results:
The results reveal significantly reduced portfolio returns, which may seem unfavorable at first glance. However, the lower sensitivity to the benchmark reflects a reduction in market exposure, aligning the portfolio with a more risk-adjusted approach rather than maximizing returns alone.
Implementation
# INSTALL REQUIRED LIBRARIES
# pip3 install yfinance --upgrade
# pip3 install statsmodels.api --upgrade
# pip3 install matplotlib
# pip3 install nbconvert # to convert the article to md later.
# IMPORT LIBARIES
import yfinance as yf
import statsmodels.api as sm
import matplotlib.pyplot as plt
# Set to display plots in Jupyter Notebook
%matplotlib inline
# Define tickers for "Magnificent 7" tech stocks and benchmark
tickers = ['AAPL', 'MSFT', 'AMZN', 'NVDA', 'GOOG', 'META', 'TSLA', 'QQQ']
#print(tickers)
# Define time period
start_date = "2022-01-01"
end_date = "2023-12-31"
# Fetch adjusted closing prices from Yahoo Finance
data = yf.download(tickers, start=start_date, end=end_date)['Adj Close']
#data.head()
# Calculate benchmark returns Nasdaq-100 ETF (QQQ), then remove QQQ from the portfolio data
benchmark_returns = data.pop('QQQ').pct_change().dropna()
# Calculate portfolio returns (sum of daily percentage changes for remaining stocks
portfolio_returns = data.pct_change().dropna().sum(axis=1)
#benchmark_returns.head()
#portfolio_returns.head()
# Linear Regression function for return analysis
def linreg(x,y):
"""Perform linear regression using OLS and return the model."""
x = sm.add_constant(x)
model = sm.OLS(y, x).fit()
return model
# Calculate alpha and beta for the unhedged portfolio
X = benchmark_returns.values.reshape(-1, 1)
Y = portfolio_returns.values.reshape(-1, 1)
model = linreg(X, Y)
alpha, beta = model.params[0], model.params[1]
#print(f'Alpha: ', alpha)
#print(f'Beta: ', beta)
# Create a hedged portfolio by adjusting portfolio returns with the beta
hedged_portfolio_returns = portfolio_returns - beta * benchmark_returns
# Calculate alpha and beta for the hedged portfolio
P = hedged_portfolio_returns.values
model_hedged = linreg(X, P)
alpha_hedged, beta_hedged = model_hedged.params[0], model_hedged.params[1]
#print(f'Alpha_Hedged: ', alpha_hedged)
#print(f'Beta_Hedged: ', beta_hedged)
# Print regression summaries
print("Unhedged Portfolio Regression Summary")
print(model.summary())
print('==============================================================================')
print(f'Unhedged Alpha: {alpha:.4f}, Unhedged Beta: {beta:.4f}\n')
print("Hedged Portfolio Regression Summary")
print(model_hedged.summary())
print('==============================================================================')
print(f'Hedged Alpha: {alpha_hedged:.4f}, Hedged Beta: {beta_hedged:.4f}\n')
# Calculate cumulative returns for both portfolios
cumulative_unhedged = (1 + portfolio_returns).cumprod() - 1
cumulative_hedged = (1 + hedged_portfolio_returns).cumprod() - 1
# Plotting the unhedged and hedged portfolio returns compared to the benchmark,
# Cumulative returns to understand the overall impact of hedging
fig, axs = plt.subplots(3, 1, figsize=(12, 15), sharex=True)
# Plot 1: Unhedget Portfolio vs Benchmark Returns
axs[0].plot(portfolio_returns, color='orange', label='Unhedged Portfolio')
axs[0].plot(benchmark_returns, color='blue', label='Benchmark')
axs[0].set_title('Unhedged - Benchmark vs Portfolio Returns')
axs[0].set_xlabel('Date')
axs[0].set_ylabel('Daily Returns in %')
axs[0].set_ylim(-0.5 , 0.5)
axs[0].legend()
axs[0].grid(True)
# Annotate unhedged alpha and beta values
axs[0].text(0.05, 0.9, f'Unhedged Alpha: {alpha:.4f}\nUnhedged Beta: {beta:.4f}',
transform=axs[0].transAxes, fontsize=10, color='red', verticalalignment='top',
bbox=dict(boxstyle='round,pad=0.5', edgecolor='black', facecolor='white'))
# Plot 2: Hedget Portfolio vs Benchmark Returns
axs[1].plot(hedged_portfolio_returns, color='green', label='Hedged Portfolio')
axs[1].plot(benchmark_returns, color='blue', label='Benchmark')
axs[1].set_title('Hedged - Benchmark vs Portfolio Returns')
axs[1].set_xlabel('Date')
axs[1].set_ylabel('Daily Returns in %')
axs[1].set_ylim(-0.5 , 0.5)
axs[1].legend()
axs[1].grid(True)
# Annotate hedged alpha and beta values
axs[1].text(0.05, 0.9, f'Hedged Alpha: {alpha_hedged:.4f}\nHedged Beta: {beta_hedged:.4f}',
transform=axs[1].transAxes, fontsize=10, color='red', verticalalignment='top',
bbox=dict(boxstyle='round,pad=0.5', edgecolor='black', facecolor='white'))
# Plot 3: Cumulative Unhedged vs Hedged Portfolio Returns
axs[2].plot(cumulative_unhedged, color='orange', label='Cumulative Unhedged Portfolio')
axs[2].plot(cumulative_hedged, color='green', label='Cumulative Hedged Portfolio')
axs[2].set_title('Cumulative Returns - Unhedged vs Hedged Portfolio')
axs[2].set_xlabel('Date')
axs[2].set_ylabel('Cumulative Returns')
axs[2].legend()
axs[2].grid(True)
plt.tight_layout()
plt.show()
# Display the plot
plt.tight_layout()
plt.show()
Unhedged Portfolio Regression Summary
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.938
Model: OLS Adj. R-squared: 0.938
Method: Least Squares F-statistic: 7587.
Date: Thu, 14 Nov 2024 Prob (F-statistic): 1.46e-303
Time: 23:57:32 Log-Likelihood: 916.28
No. Observations: 500 AIC: -1829.
Df Residuals: 498 BIC: -1820.
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
——————————————————————————
const 0.0013 0.002 0.740 0.460 -0.002 0.005
x1 9.1878 0.105 87.103 0.000 8.981 9.395
==============================================================================
Omnibus: 49.341 Durbin-Watson: 1.978
Prob(Omnibus): 0.000 Jarque-Bera (JB): 244.914
Skew: -0.217 Prob(JB): 6.57e-54
Kurtosis: 6.401 Cond. No. 60.8
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
==============================================================================
Unhedged Alpha: 0.0013, Unhedged Beta: 9.1878
Hedged Portfolio Regression Summary
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.000
Model: OLS Adj. R-squared: -0.002
Method: Least Squares F-statistic: 7.377e-14
Date: Thu, 14 Nov 2024 Prob (F-statistic): 1.00
Time: 23:57:32 Log-Likelihood: 916.28
No. Observations: 500 AIC: -1829.
Df Residuals: 498 BIC: -1820.
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
——————————————————————————
const 0.0013 0.002 0.740 0.460 -0.002 0.005
x1 -3.58e-15 0.105 -3.39e-14 1.000 -0.207 0.207
==============================================================================
Omnibus: 49.341 Durbin-Watson: 1.978
Prob(Omnibus): 0.000 Jarque-Bera (JB): 244.914
Skew: -0.217 Prob(JB): 6.57e-54
Kurtosis: 6.401 Cond. No. 60.8
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
==============================================================================
Hedged Alpha: 0.0013, Hedged Beta: -0.0000
Hedged vs Unhedged Portfolio
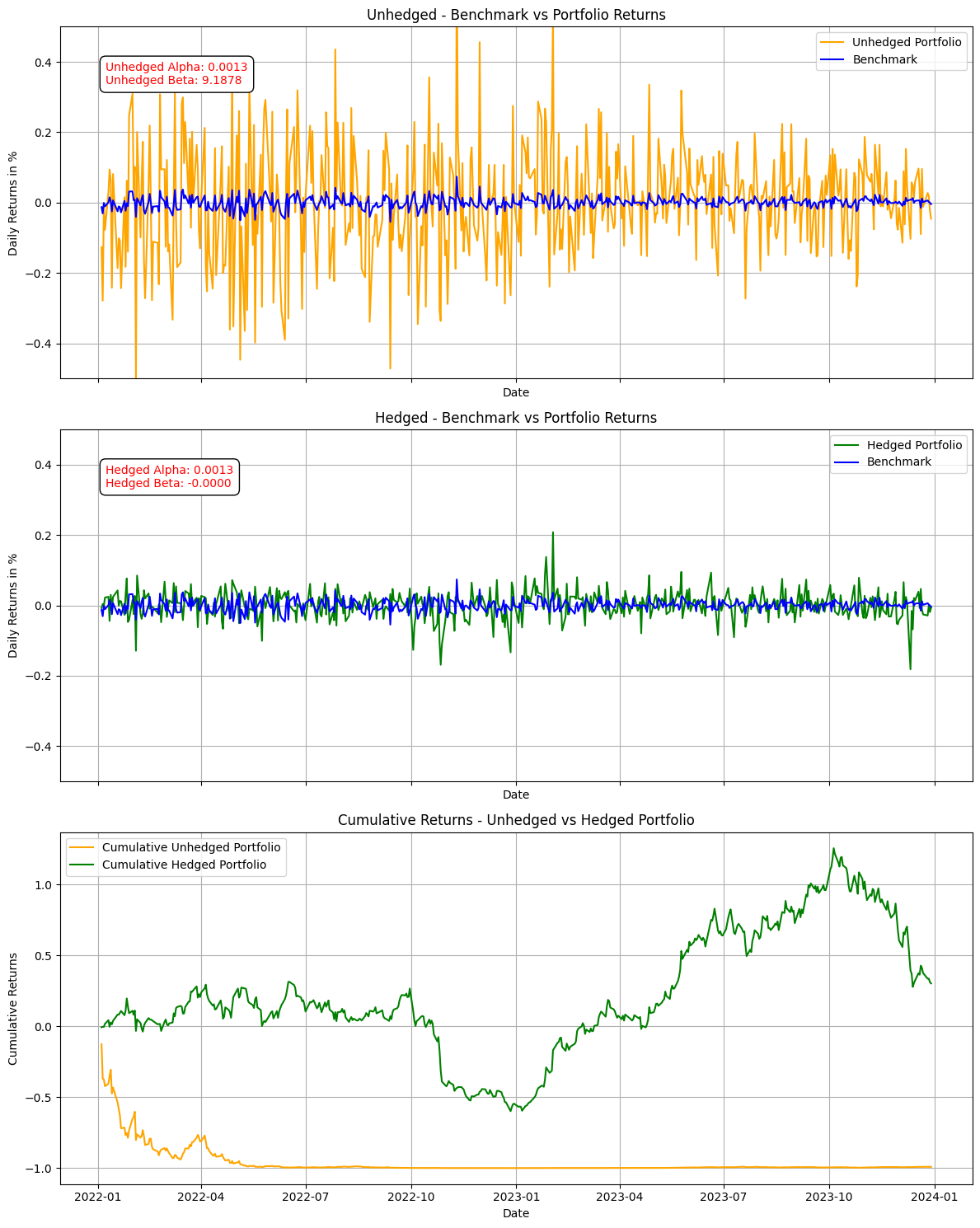
Understanding how hedging impacts portfolio performance can be an essential tool in navigating volatile markets. By exploring and adjusting our portfolios with strategies like beta-adjusted hedging, we’re able to balance returns with risk exposure effectively. Whether you’re managing individual investments or larger funds, having a structured approach to volatility can be a real game-changer.
Experiment Further:
There’s so much more to uncover!
We can try modifying the tickers in the code to explore different stocks and see how alpha and beta values vary.
We can also test different time periods to observe how changing market conditions affect our analysis and risk metrics.
This exercise will provide better insights into how beta and hedging strategies vary across portfolios and economic contexts.
Thanks for reading! I look forward to hearing your thoughts and any strategies you use for risk-adjusted returns.
APPENDIX
Alternative Portfolios
We can experiment the hedging impact with alternative portfolios using the following portfolios. Here’s a list of sample portfolios to save you time.
| Portfolio Name | Companies Included | Description |
|---|---|---|
| MAG-7 | Microsoft, Apple, Google (Alphabet), Meta, Amazon, Nvidia, Tesla | The seven largest U.S. tech and growth companies, leading innovation in various sectors. |
| FAANG | Facebook (Meta), Apple, Amazon, Netflix, Google (Alphabet) | A group of influential U.S. tech companies, initially popularized for high-growth potential. |
| MANGA | Microsoft, Apple, Nvidia, Google (Alphabet), Amazon | Dominant players in cloud, AI, and consumer tech markets with strong growth and influence. |
| TAND | Tesla, Apple, Nvidia, Disney | Focuses on companies leading in electric vehicles, consumer tech, entertainment, and AI. |
| MAAN | Microsoft, Apple, Amazon, Nvidia | Major players in cloud computing, AI, and hardware, key drivers of tech advancements. |
| FANTASY | Facebook (Meta), Amazon, Netflix, Tesla, Alphabet, Salesforce, Zoom | High-growth, innovative companies in social media, streaming, EVs, cloud, and video tech. |
| BAT | Baidu, Alibaba, Tencent | China’s major tech giants, excelling in search engines, e-commerce, and social media. |
For each portfolio, we should be using the corresponding benchmark for efficient hedging.
| Portfolio | Benchmark | Explanation |
|---|---|---|
| MAG7 | Nasdaq-100 (QQQ) | Contains the largest U.S. tech companies, which make up a large part of the Nasdaq-100. |
| FAANG | S&P 500 (SPY) | The FAANG stocks are part of the broader U.S. market, and the S&P 500 is widely considered the benchmark for large-cap U.S. equities. |
| MANGA | Nasdaq-100 (QQQ) | Primarily tech-focused with large-cap U.S. companies that align closely with the Nasdaq-100. |
| TAND | Nasdaq-100 (QQQ) | All companies are in the technology and communication sectors, heavily weighted in the Nasdaq-100. |
| MAAN | Nasdaq-100 (QQQ) | Another portfolio dominated by large-cap U.S. tech stocks. |
| FANTASY | Nasdaq-100 (QQQ) or ARK Innovation ETF (ARKK) | Contains high-growth, disruptive companies, similar to those in ARKK’s innovation-focused portfolio. |
| BAT | Hang Seng Tech Index (HSTECH) | Consists of leading Chinese tech companies, which align with the Hang Seng Tech Index in Hong Kong or MSCI China. |
# List of Sample Portfolios with their benchmarks provided for further testing, by assigning these portfolios to `tickers`
MAG7 = ['MSFT', 'AAPL', 'GOOG', 'META', 'AMZN', 'NVDA', 'TSLA', 'QQQ']
FAANG = ['META', 'AAPL', 'AMZN', 'NFLX', 'GOOG', 'SPY']
MANGA = ['MSFT', 'AAPL', 'NVDA', 'GOOG', 'AMZN', 'QQQ']
TAND = ['TSLA', 'AAPL', 'NVDA', 'DIS', 'QQQ']
MAAN = ['MSFT', 'AAPL', 'AMZN', 'NVDA', 'QQQ']
FANTASY=['META', 'AMZN', 'NFLX', 'TSLA', 'GOOG', 'CRM', 'ZM', 'ARKK']
BAT = ['BIDU', 'BABA', 'TCEHY', 'HSTECH']
# List of Sample benchmarks
benchmark_list = ['QQQ', 'SPY', 'ARKK', 'HSTECH']
End of Post